Momento d’inerzia: definizioni ed equazioni

Il termine “momento d’inerzia” è spesso usato con un significato generico ma, a seconda del contesto, può indicare tre diversi momenti d’inerzia: di massa, planare o polare. Per sapere quale di questi valori è necessario per un determinato calcolo o analisi, è importante capire come si differenziano e la loro relazione con il comportamento di un oggetto.

Momento d’inerzia di massa

Il momento d’inerzia di massa descrive la capacità di un oggetto di resistere all’accelerazione angolare, che dipende da come la massa dell’oggetto è distribuita rispetto all’asse di rotazione (cioè la forma dell’oggetto). Il momento d’inerzia della massa è solitamente indicato con il simbolo “I”. Tuttavia, in ambito tecnico, viene comunemente utilizzato il simbolo “J”, ad esempio nelle specifiche di inerzia di motori e riduttori. L’unità di misura è la massa moltiplicata per la distanza al quadrato: kg m² o lbm-ft² (si noti che a volte si usa anche slug-ft²).

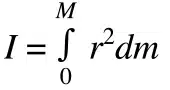
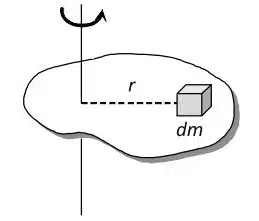
In molte applicazioni, un oggetto è costituito da un centro di massa. Il momento d’inerzia della massa è semplicemente la massa dell’oggetto moltiplicata per il raggio (distanza dall’asse di rotazione) al quadrato.

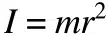
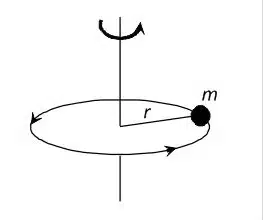
Il momento d’inerzia della massa è importante per il dimensionamento del motore. Il rapporto di inerzia (rapporto tra l’inerzia del carico e l’inerzia del motore) è importante per determinare se il motore può controllare efficacemente l’accelerazione e la decelerazione del carico.

Momenti d’inerzia planari e polari

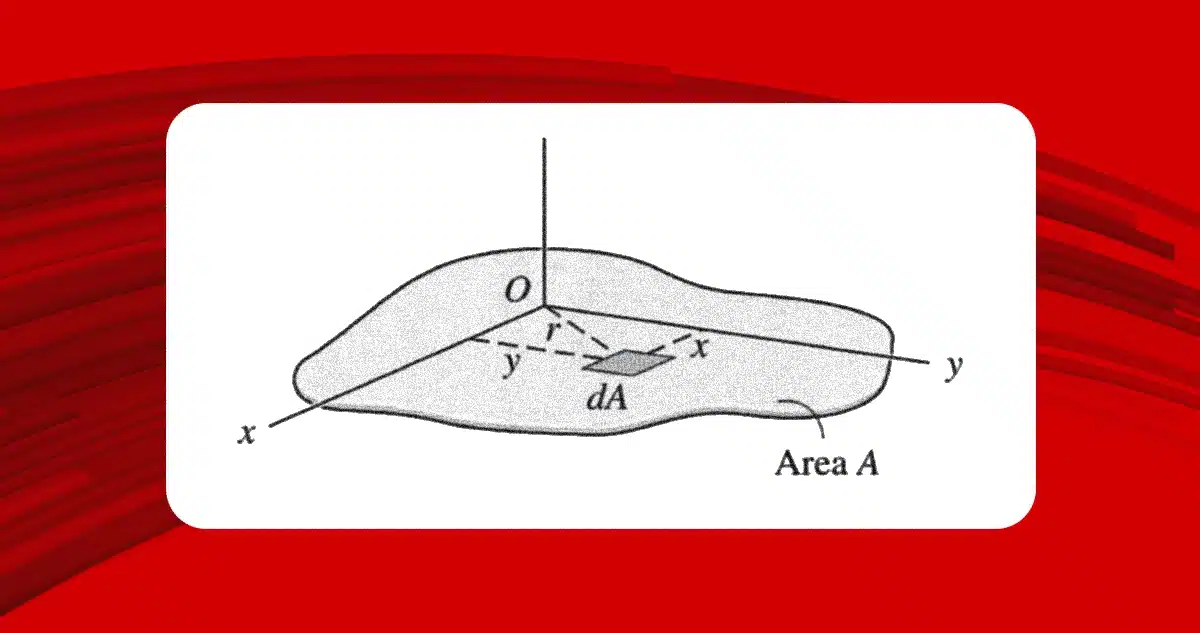
I momenti d’inerzia planari e polari rientrano nel cosiddetto “secondo momento d’inerzia”. Il momento d’inerzia planare descrive la distribuzione di un’area rispetto a un asse di riferimento (di solito l’asse baricentrico o centrale). Questo elemento è importante perché identifica la resistenza dell’area alla flessione.

L’equazione del momento d’inerzia planare utilizza l’integrale secondo della distanza rispetto al piano di riferimento e lo moltiplica per l’elemento differenziale dell’area. Il risultato è espresso in unità di lunghezza alla quarta potenza: m⁴ o in⁴.

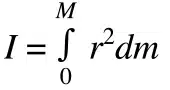
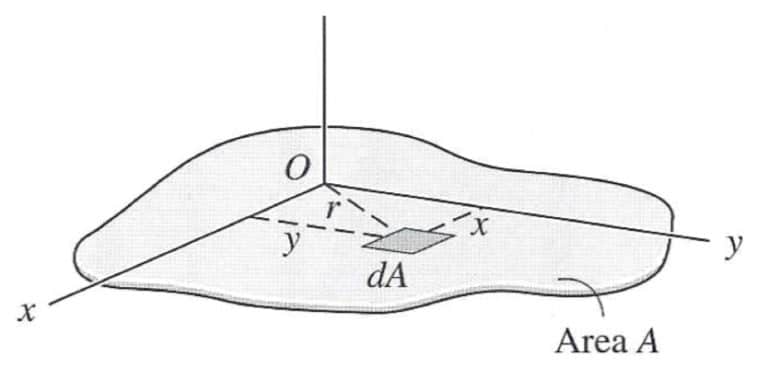
Il momento d’inerzia polare è analogo al momento d’inerzia planare, ma si applica a oggetti cilindrici e descrive la loro resistenza alla torsione (generata da una coppia applicata).

L’equazione per il momento d’inerzia polare è essenzialmente la stessa del momento d’inerzia planare. Tuttavia, per il momento d’inerzia polare, la distanza è misurata rispetto a un asse parallelo alla sezione trasversale dell’area. Il momento d’inerzia polare è talvolta indicato con la lettera J invece che con il simbolo I, ma le unità di misura sono le stesse del momento d’inerzia planare: m4 o in⁴.

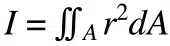
Il momento d’inerzia polare (qui indicato come Iᵖ) può essere calcolato anche sommando i momenti d’inerzia planari x e y (Iˣ e Iʸ).

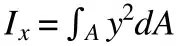
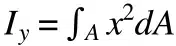
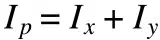
I momenti d’inerzia planari e polari sono utilizzati per calcolare la flessione, sia lo spostamento lineare dovuto a una forza applicata sia lo spostamento angolare risultante da un momento applicato.